Introduction (Top)
In this section, we provide a general assessment of the DR1 data quality including astrometric and photometric precision, imaging depth in terms of measurement signal-to-noise and object detection completeness, morphological object classification accuracy, and the identification and removal of likely artifacts.
Astrometry (Top)
The DR1 astrometric solution is derived in two steps using SCAMP with 2MASS as the reference catalog (Morganson et al. 2018). At the single-epoch stage, we find internal astrometric uncertainties of 42, 36, 37, 39, and 56 mas in the g, r, i, z, and Y bands, respectively, as determined from the median of two-dimensional angular separations between repeated measurements of bright stars from individual exposures. Following the astrometric refinement step for image coaddition by SCAMP, the estimated internal astrometric precision for the coadd is ~30mas RMS (median over coadd tiles). The absolute astrometric uncertainty of the coadd is evaluated with respect to Gaia DR1 (Gaia Collaboration et al. 2016).
Figure 1 shows that the residuals are smallest in regions with with larger stellar densities closer to the Galactic plane (for comparison, see Figure 10 ), and the mean over the footprint is ~145 mas. Further details of astrometric calibration, including ongoing development using Gaia as a reference catalog, are provided in Bernstein et al. (2017b).
Figure 1. Absolute astrometric precision (total distance) measured using Gaia DR1 stars with GGaia ~ 16 as an external reference. Left: Mean value of the astrometric discrepancy with respect to Gaia versus sky position computed within HEALPix cells of resolution nside = 256. Right: Normalized histogram showing the distribution of astrometric offsets
Photometry (Top)
The relative top-of-the-atmosphere flux measurements for astronomical sources in DR1 have been calibrated using a forward modeling technique to account for both atmospheric and instrumental components of the total system throughput (FGCM; Burke et al. 2017). The parameters of the model were initially fit from observations taken in photometric conditions to establish a network of calibration stars that spans the full survey footprint. This network was subsequently used to refine the calibration of exposures taken in non-photometric conditions. Meanwhile, the absolute photometric calibration of DR1 is tied to the spectrophotometric Hubble CALSPEC standard star C26202 (Bohlin et al. 2014) located in the SN field C3.
Several hundred repeated measurements of C26202 in a variety of conditions yielded a set of small shifts (3 mmag) to place the DES photometry on the AB system. These shifts have been pre-applied to the DR1 zeropoints. The statistical uncertainties on these shifts are estimated to be 2.6, 2.9, 3.4, 2.5, and 4.5 mmag for the g, r, i, z, and Y bands, respectively. Additional sources of systematic uncertainty on the absolute photometric calibration could arise from uncertainty in the level of out-of-band light leakage and uncertainty in the synthetic photometry of C26202. We are currently undertaking observations and analysis of two additional HST CALSPEC standards to reduce the systematic uncertainty of the AB offsets. We reproduce below several of the key results from Burke et al. (2017) regarding the relative photometric calibration.
Figure 2. Statistical uncertainty of coadd zeropoints in the i-band estimated from the FGCM photometric calibration. Left: Mean value of the uncertainty vs. sky position, computed within HEALPix cells of resolution nside = 256. Right: Normalized histogram showing the distribution of zeropoint uncertainties over the footprint.
Figure 3. The distribution of photometric residuals against Gaia’s G band (mag units) across the DES footprint is used the evaluate the uniformity of the coadd FGCM calibration. Left: Mean value of this residual vs sky position in a HEALPix cell of nside = 256. Right: Normalized histogram of photometric residuals over the footprint.
The single-epoch photometric statistical precision (associated with random errors in the FGCM fit parameters) derived from repeated measurements of FGCM calibration stars is 7.3, 6.1, 5.9, 7.3, 7.8 mmag in the g, r, i, z, and Y bands, respectively. Under the assumption that successive tiled observations of the same fields yield largely independent model fit parameters (as would be expected from the widely spaced observations in DES), we estimate the statistical precision of coadd zeropoints by combining the fit results from overlapping exposures. The median coadd zeropoint statistical uncertainty for the g, r, i, z, and Y band is 5, 4, 5, 6, and 5 mmag, respectively. Figure 2 shows an example distribution for the i band. As a validation, we compare the photometric uniformity of DES DR1 to the space-based Gaia G-band photometry (Figure 3). Variations in uniformity are found to be 6.6 mmag, as estimated from a Gaussian fit to the offset distribution between GGaia and Gpred(r) predicted from the DES r-band.
To account for extinction from interstellar dust, we include an additional column in the DR1 photometry tables for E(B - V) values from the reddening map of Schlegel et al. (1998) (SFD98) at the location of each catalog object. The E(B -V) values were obtained using a linear interpolation of the Zenithal Equal Area projected map distributed by SFD98. We computed fiducial interstellar extinction coefficients, Rb, for each band so that the corrections to the FGCM calibrated source magnitudes are Ab = E(B -V)Rb. Fiducial coefficients are derived using the Fitzpatrick (1999) reddening law with RV = 3.1 and the Schlafly & Finkbeiner (2011) calibration adjustment to the original SFD98 reddening map (N = 0.78). Note that the Schlafly & Finkbeiner (2011) calibration adjustment is included in our fiducial reddening coefficients; these coefficients are intended to be used directly with E(B -V) values from the original SFD98 reddening map. We integrated over the DR1 Standard Bandpasses considering a fixed source spectrum that is constant in spectral flux density per unit wavelength, and adopted the low-extinction limit. The latter simplification is appropriate for DES, for which E(B-V) < 0.1 mag over ~99% of the footprint. The resulting multiplicative coefficients for each band, Rb, are 3.186, 2.140, 1.569, 1.196 and 1.048 in the g, r, i, z and Y bands, respectively. The DES science team continues to explore systematic uncertainties associated with interstellar extinction modeling.
Flagged objects (Top)
For coadd objects, if any pixel is masked in all of the contributing exposures for a given band, the IMAFLAGS_ISO = 1 flag is set for that band. This flag is predominantly set for saturated objects and objects with missing data. We recommend a baseline quality criteria of IMAFLAGS_ISO = 0 (in the relevant bands) for most science applications since the majority of flagged objects have unreliable photometry. The DES DR1 catalog also includes other standard flags FLAGS provided by the SExtractor pipeline.
The effective depth of the DES DR1 wide-field coadd catalog is dependent on the photometric measurement of interest and can be quantified through various approaches. Here we derive simple depth estimates from the flux distribution of cataloged objects, the magnitude corresponding to a fixed signal-to-noise threshold (S/N = 10), an aperture estimate from the input imaging, and object detection completeness. In general, the type of source and surface brightness must also be considered when evaluating the survey depth. The settings used for the source extraction and deblending steps of the DESDM pipeline allow for efficient detection of objects with S/N ~10 in the r +i+z composite detection image (Morganson et al. 2018). At the bright end, saturation effects start to become important at r < 16. For even brighter magnitudes, the fraction of saturated objects increases until objects are no longer cataloged due to pixel-level masking applied during processing. For each of the depth studies considered here, we selected a sample of high-quality DR1 coadd objects with using FLAGS_[GRIZ] < 4 and IMAFLAGS_ISO_[GRIZ] = 0. Below we describe these different approaches to estimate the depth of DR1.
Table 1. DES DR1 coadd catalog depth estimates
| Method |
g |
r |
i |
z |
Y |
| Maximum in number counts (MAG_AUTO) |
24.32 |
23.89 |
23.41 |
22.09 |
21.40 |
| Imaging depth from mangle (MAG_APER_4) |
24.28 |
23.95 |
23.34 |
22.63 |
21.38
|
|
Measured with S/N = 10 (MAG_APER_4)
|
24.33 |
24.08 |
23.44 |
22.69 |
21.44 |
| Measured with S/N = 10 (MAG_AUTO) |
23.52 |
23.10 |
22.51 |
21.81 |
20.61 |
| Detection completeness of 95% (MAG_AUTO) |
23.72 |
23.35 |
22.88 |
22.25 |
... |
Figure 4. Normalized histograms of source counts binned by SExtractor’s MAG_AUTO quantity showing the flux distribution of detected sources.
Flux Distribution
The distribution of astronomical sources is weighted towards low-flux sources. A faint limit on the source detection threshold can be estimated from the mode of the number counts distribution of sources as a function of magnitude. Figure 4 shows the number counts of coadd objects as a function of MAG_AUTO in all five DES bands. The mode of the MAG_AUTO distribution is 24.32, 23.89, 23.41, 22.09, 21.40 in the g, r, i, z, and Y bands, respectively. No restriction were placed on source morphology (i.e., stars vs. galaxies) for this estimate.
Magnitude limit at fixed signal-to-noise
The magnitude limit corresponding to a fixed signal-to-noise for a given photometric measurement (e.g., MAG_AUTO) can be empirically determined from the distribution of magnitude uncertainties as a function of magnitude (Rykoff et al. 2015). SExtractor provides an estimate of the photometric uncertainty through the MAGERR quantities, which are estimated from the fluctuations of the background around the sources. These are related to signal-to-noise, δF/F, via the differentiation of Pogson’s law (Pogson 1856):
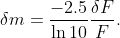
We summarize in Table 2 the characteristic S/N = 10 thresholds for MAG_AUTO corresponding to δF/F ~0.1 in each of the g, r, i, z, and Y bands. Figure 5 shows the MAG_AUTO distribution for DES DR1 catalog objects with 0.10837 < MAGERR_AUTO < 0.10877. The spread in these distributions represents comes from the dependence of S/N on source properties (e.g., surface brightness) and survey non-uniformity.
Depth from image properties
It is also possible to estimate the DES DR1 imaging depth using mangle (Hamilton & Tegmark 2004, Swanson et al. 2008), which generates a vectorized map of the survey coverage accounting for the focal plane geometry and imaging artifacts (i.e., bright star masks, bleed trails, satellite trails) (Drlica-Wagner et al. 2017, Morganson et al. 2018). The mangle processing produces a coadd weight map from a weighted sum of the single-epoch input images. This weight was converted to a the S/N = 10 limiting magnitude for a 2'' diameter aperture, corresponding to the MAG_APER_4 quantity measured by SExtractor (for details, see Drlica-Wagner et al. 2017). The median limiting magnitude in the g, r, i, z, and Y bands across the DES footprint is 23.52, 23.10, 22.51, 21.81, 20.61, respectively (Figure 6).
Figure 5. Catalog depth estimated for MAG_AUTO using catalog objects with S/N = 10 (MAGERR_AUTO = 0.10857.
Figure 6. Catalog depth estimated for a 1.95'' aperture (MAG_APER_4) using mangle.
Object detection completeness
Another measure of effective imaging depth is the object detection completeness relative to deeper imaging data. We evaluated the detection completeness of DES DR1 through a comparison to public CFHTLenS data (Erben et al. 2013) using an overlap region centered on (Ra;Dec) = (34.5;-5.4) consisting of 9 CFHTLenS fields in the W1 patch. The CFHTLens 5σ magnitude limits in a 2'' aperture for g', r', i', y' and z' are 25.58, 24.88, 24.54, 24.71 and 23.46, respectively. To ensure full coverage in both surveys, we restricted the analysis to regions with CFHTLenS image mask value MASK = 0 and DES coverage fraction > 99% in the intersection of the griz bands (see Drlica-Wagner et al. 2017). The effective area of overlap in both surveys including masking is 6.0 sq. deg.
Object matching is performed using a 1'' radius and we require a robust flux measurement in the respective DES band (15 < MAG_AUTO < 30) that is roughly consistent with that of CFHTLenS (within 1 mag) for an object to count as “detected” in DES DR1.
The DES DR1 detection efficiency is defined as the fraction of CFHTLenS objects in a given flux interval that have a matched DES object passing the baseline quality cuts listed above, and is expressed in the DES photometric system using converted flux measurement from CFHTLenS. The resulting detection efficiency curves are plotted in Figure 7. DES DR1 detection efficiencies are only plotted for the magnitude range brighter than the typical S/N = 5 limiting magnitude of CFHTLenS. The 95% completeness magnitude thresholds obtained from this test in the g, r, i, and z bands are 23.72, 23.35, 22.88, and 22.25, respectively. CFHTLenS does not include comparable Y-band coverage.
Using the same baseline quality selection criteria of FLAGS_[GRIZ] < 4 and IMAFLAGS_ISO_[GRIZ] = 0, we find that in each of griz bands, that roughly less than 1% of DES objects with MAG_AUTO greater than 20 and less than the typical S/N = 5 limiting magnitude of CFHTLenS lack a matched counterpart in CFHTLenS (Figure 7). This suggests that contamination from spurious objects in DES DR1 is also roughly 1%.
Morphological object classification (Top)
A basic selection on object size relative to the PSF can be used to separate samples of spatially extended galaxies from point-like stars and quasars. Accurate object classification becomes challenging for ground based imaging surveys at faint magnitudes, and accordingly, optimal use of morphological, color, and temporal information is an active area of research (e.g., Fadely et al. 2012, Małek et al. 2013, Kim et al. 2015, Kim & Brunner 2017). Several object classification schemes have been applied to DES data for a variety of science cases (e.g., Soumagnac et al. 2013, Chang et al. 2015, Reed et al. 2015, Drlica-Wagner et al. 2017).
The most common classification scheme makes use of the SExtractor SPREAD_MODEL, which compares the fit of a local PSF model to a slightly extended exponential disk model (Desai et al. 2012). Below we show a example using SPREAD_MODEL for object classification in a way that is suitable for both stellar and extragalactic science.
We define a new variable EXTENDED_COADD as the independent sum of several Boolean conditions:
EXTENDED_COADD =
((SPREAD_MODEL_I+ 3 × SPREADERR_MODEL_I) > 0.005)
+ ((SPREAD_MODEL_I+SPREADERR_MODEL_I) > 0.003)
+ ((SPREAD_MODEL_I-SPREADERR_MODEL_I) > 0.003)
Note that EXTENDED_COADD is defined by a sequence of boolean conditions that, when true, add a unit to the classifier. This classifier results in a value of 0 (high-confidence stars), 1 (likely stars), 2 (mostly galaxies), and 3 (high-confidence galaxies).
Figure 7. DES DR1 detection efficiency and contamination relative to deeper imaging from CFHTLenS. Solid color curves represent the detection efficiency, while dashed color curves show the fraction of unmatched objects appearing only in DES. For visual reference, gray dashed lines indicate 5% and 95% of objects
Figure 8. Stars and galaxies occupy distinct regions of spreadmodel-space at bright magnitudes, but become more difficult to distinguish at faint magnitudes
We evaluate the performance of the example classifier above using three regions in the main body of the DES footprint that overlap fields from HSC-SSP DR1 (Aihara et al. 2017b) with typical seeing in the i-band FWHM ~ 0.7'': SXDS (Ultra Deep layer), DEEP2_3 (Deep layer), and portions of VVDS (Wide layer). The areal overlap between these HSC-SSP data sets and DES is ~18 deg2. The HSC-SSP data are of sufficient depth and image quality that a distinct stellar locus is clearly visible in the HSC concentration parameter IMAG_PSF - ICMODEL_MAG to an i-band magnitude of ~24.0. We choose empirically an interval of EXTENDED_COADD values to select stellar or galactic samples with a balance of classification efficiency and purity appropriate for different science cases (Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12). For instance, one can define galaxy (EXTENDED_COADD >= 2) and stellar samples (EXTENDED_COADD <= 1) having ~310M and ~80M objects, respectively, following the standard object quality selection.
Figure 9. DES DR1 object classification accuracy versus HSC-SSP for the stellar sample. By using an interval of EXTENDED_COADD values, the balance of classification efficiency and purity can be adjusted as appropriate for specific science cases.
Figure 10. Stellar density map at HEALPix NSIDE = 1024 resolution created with the EXTENDED_COADD = 0 selection described above. Discrete peaks in the stellar density correspond to globular clusters and dwarf galaxies in the Milky Way halo.
Figure 11. DES DR1 object classification accuracy versus HSC-SSP for the galaxy sample. By using an interval of EXTENDED_COADD values, the balance of classification efficiency and purity can be adjusted as appropriate for specific science cases.
Figure 12. Galaxy density map at HEALPix NSIDE = 1024 resolution created with the EXTENDED_COADD = 3 selection described above.
Table 2. Stellar classification accuracy quantified as the area under the ROC curve (AUC) in three flux intervals, using HSC-SSP as a reference (see Figure 13). In this case, the AUC statistic is the probability that the simple classifier will correctly rank a randomly chosen star higher than a randomly chosen galaxy.
| Quantity |
WAVG_SPREAD_MODEL |
SPREAD_MODEL |
CLASS_STAR |
| 21.5 < MAG_AUTO_I < 22.0 |
0.994
|
0.991
|
0.979
|
| 22.0 < MAG_AUTO_I < 22.5 |
0.981 |
0.981 |
0.954 |
| 22.5 < MAG_AUTO_I < 23.0 |
0.917 |
0.948 |
0.881 |
We recommend using quantities based on SExtractor SPREAD_MODEL for morphological classification in DR1. Although the SExtractor quantity CLASS_STAR has been commonly used in the past, we find that SPREAD_MODELbased classifiers consistently outperform CLASS_STAR, as exemplified by the receiver operating characteristic (ROC) curve shown in Figure 13 and summarized in Table 2. The ROC curves are generated by performing a simple scan of threshold values for each of SExtractor quantities, and using the HSC-SSP classifications described above as a reference. Classifiers based on the weighted averaged SPREAD_MODEL from single epoch detections, WAVG_SPREAD_MODEL, are expected to be more robust for objects that are bright enough to be detected in single-epoch imaging. It is expected that classifiers using alternative bands and/or combinations of object measurements will be more appropriate for specific science cases.
Figure 13. Receiver operating characteristic (ROC) curve for a stellar selection in the magnitude range 22.0 < MAG_AUTO_I < 22.5. The SPREAD_MODEL outperforms CLASS_STAR in classification accuracy of DES DR1 objects with respect to HSC-SSP.







